[The link bar feature is not available in this web] ||| Natrag: Crtanje primitivnih oblika | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje trodimenzionalnih tijela |
U mnogim primjenama računarske grafike potrebno je prikazati različite vrste površina u trodimenzionalnom prostoru. Modeliranje površina složen je zadatak i postoji više načina. Najčešće korišteni načini temelje se na primjeni:
parametarskih površina,
mreža mnogokuta,
površina drugog reda.
Parametarske površine predstavljaju generalizaciju parametarskih krivulja na način da se umjesto jednog parametra koriste dva. Mreža mnogokuta predstavlja skup povezanih mnogokutnih ravnih površina kojima se aproksimira željena površina proizvoljnog oblika. Površine drugog reda su površine definirane općom jednadžbom drugog reda u implicitnom obliku. U nastavku ćemo definirati ove načine modeliranja površina u trodimenzionalnom prostoru.
Dvoparametarske površine trećeg reda predstavljaju generalizaciju parametarskih
krivulja trećeg reda. U jednadžbi parametarske krivulje
![]() parametar t zamijenimo parametrom s, a zatim učinimo geometrijski vektor G
promjenljivim u 3D prostoru duž nekog puta u ovisnosti o parametru t,
parametar t zamijenimo parametrom s, a zatim učinimo geometrijski vektor G
promjenljivim u 3D prostoru duž nekog puta u ovisnosti o parametru t,
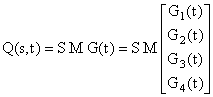
Za izabranu vrijednost t=t1 izraz Q(s,t1) definira krivulju trećeg reda. Za niz bliskih vrijednosti parametra t izraz Q(s,t) definira niz bliskih krivulja trećeg reda koje definiraju površinu. Gi(t) su krivulje trećeg reda:
![]()
gdje je
![]()
Uvrštenjem ovih izraza za Gi(t) i Gi u izraz za Q(s,t) dobija se sljedeći oblik
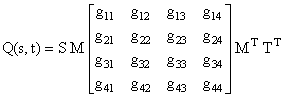
koji se može sažeto napisati u sljedećem obliku:
![]() 0 £
s,t £
1
0 £
s,t £
1
Ova jednadžba može se ispisati i posebno za svaku koordinatu:
![]()
![]()
![]()
Ako u općem izrazu za dvoparametarsku krivulju trećeg reda uvrstimo Bezierovu baznu matricu MB i Bezierovu geometrijsku matricu GB dobivamo izraze za Bezierove površine:
![]()
![]()
![]()
Bezierova geometrijska matrica sastoji se od 16 kontrolnih točaka (slika 3.15).
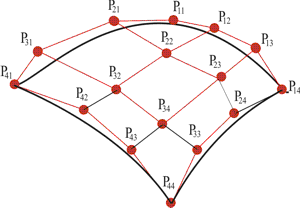
Slika 3.15 16 kontrolnih točaka Bezierove površine.
Bezierove površine su prikladne za interaktivno crtanje (jer su vektori smjera tangenti u krajnjim točkama eksplicitno izraženi). Uvjet za C0 i G0 kontinuitet na spojevima dijelova površina je jednakost rubnih kontrolnih točaka. Uvjet za G1 kontinuitet je kolinearnost četiri skupa točaka koji uključuju rubne i susjedne kontrolne točke (slika 3.16).
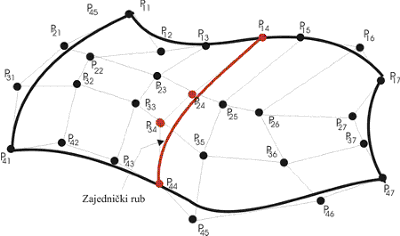
Slika 3.16 Spoj dvaju segmenata Bezierove površine.
Kao i u slučaju crtanja parametarskih krivulja, osnovni pristupi crtanju parametarskih površina uključuju itrativni i rekurzivni postupak.
Iterativni postupak podrazumijeva proračun polinoma trećeg reda za niz bliskih rastućih vrijednosti parametara t i s. Mogući pristup je iscrtavanje niza krivulja kao funkcija parametra t (dok se vrijednost parametra s drži konstantnom za pojedinu krivulju, a mijenja se od krivulje do krivulje). Zatim se iscrtava niz krivulja kao funkcija parametra s (dok se vrijednost parametra t drži konstantnom za pojedinu krivulju, a mijenja se od krivulje do krivulje). Ovaj postupak ilustriran je na slici 3.17. U slučaju primjene iterativnog proračuna, znatno veći broj proračuna nego kod krivulja još više ističe važnost optimiziranih numeričkih algoritama.
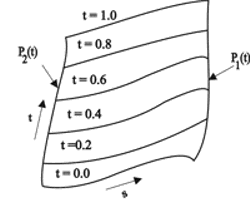
Slika 3.17 Postupak iterativnog pristupa crtanju površine.
Postupak rekurzivne podjele podrazumijeva dijeljenje površine na četverokute (omeđene krivuljama) do zadovoljavajuće ravnoće rezultirajućih četverokuta. Podjela se obavlja dijeljenjem prvo po jednom, a zatim po drugom parametru. Dijeljenje se obavlja crtanjem krivulje po jednom parametru uz konstantnu vrijednost drugog parametra. Konstantna vrijednost drugog parametra određuje se kao aritmetička sredina između vrijednosti tog parametra koje su korištene u prethodnoj podjeli. Ovaj postupak ilustriran je na slici 3.18.
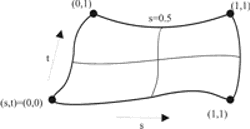
Slika 3.18 Postupak rekurzivnog pristupa crtanju površine.
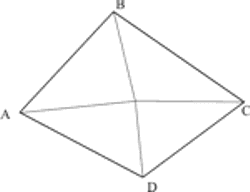
Ovaj postupak najjednostavniji je za slučaj Bezierovih površina. Kriterij ravnoće je sljedeći: udaljenost svake od 13 kontrolnih točaka do ravnine koju definiraju 3 krajnje točke mora biti manja od zadane vrijednosti. Četverokut zadovoljavajuće ravnoće dijeli se na četiri trokuta koji se ispunjavaju (slika 3.19).
Mreža mnogokuta je skup bridova, vrhova i mnogokuta povezanih tako da oblikuju površinu koja dovoljno dobro aproksimira željenu površinu. Pri tome svaki brid zajednički je za najviše dva mnogokuta, a svaki vrh zajednički je za najmanje dva brida. Svaki brid povezuje dva vrha. Mnogokut je zatvoreni skup povezanih bridova (stranica). Primjer prikaza trodimenzionalnog objekta pomoću mreže mnogokuta prikazan je na slici 3.20.
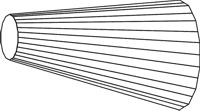
Slika 3.20 Primjer prikaza trodimenzionalnog objeklta pomoću mreže mnogokuta.
Postoji više načina za definiranje podataka o mreži mnogokuta, a temeljna razlika je u odnosu prema dva međusobno suprotstavljena kriterija: minimizaciji memorijskih zahtjeva i minimizaciji računske složenosti. Izbor između ovih pristupa ovisi o važnosti koja se u pojedinoj primjeni pridaje svakom od navedenih kriterija.
Općenito, što je prikaz eksplicitniji, računska složenost je manja, ali su potrebe za memorijskim prostorom veće. Tipične vrste operacija koje je potrebno obavljati pri crtanju mreže mnogokuta uključuju: određivanje svih bridova koji izlaze iz promatranog vrha, određivanje svih mnogokuta kojima je promatrani brid ili vrh zajednički, određivanje svih vrhova kojima je promatrani brid zajednički i iscrtavanje mreže. Najčešće korišteni načini prikazivanja modela mreže mnogokuta su:
eksplicitni način,
struktura pokazivača na listu vrhova,
struktura pokazivača na listu bridova.
U eksplicitnom
prikazu svaki je mnogokut predstavljen listom koordinata vrhova:
P = ((x1,
y1, z1), (x2, y2, z2),
...,(xn, yn, zn))
Vrhovi su u ovom prikazu poredani redom iscrtavanja. Nedostatak ovog pristupa je u tome što se vrhovi pojavljuju više puta jer ne postoji eksplicitna predstava zajedničkih vrhova. Npr. za pomicanje (npr. pomoću miša) jednog vrha nužno je identificirati sve mnogokute povezane s tim vrhom. U tu svrhu nužno je usporediti sve koordinate vrhova u jednom mnogokutu s koordinatama vrhova u svim drugim mnogokutima. Pored toga i svi zajednički bridovi se iscrtavaju dva puta.
U
prikazu temeljenom na strukturi pokazivača na listu vrhova svaki vrh se
pohranjuje samo jednom u listu vrhova
V = ((x1,
y1, z1), (x2, y2, z2),
...,(xn, yn, zn))
Mnogokut se definira listom pokazivača (indeksa) u listu vrhova (ova metoda koristi se u SPHIGS standardu). Memorijski zahtjevi su znatno manji nego u eksplicitnom prikazu. Osim toga i promjena koordinata jednog vrha je jednostavna jer nije potrebno uspoređivanje i pretraživanje. Međutim, u ovom prikazu teško je odrediti mnogokute koji imaju zajednički vrh, a i zajednički bridovi se iscrtavaju dva puta. Ova metoda ilustrirana je primjerom na slici 3.21.
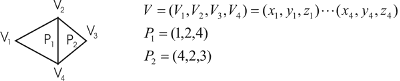
Slika 3.21 Mreža mnogokuta definirana pokazivačima u listu vrhova.
Navedeni
problemi otklonjeni su u prikazu temeljenom na strukturi pokazivača u listu
bridova. U ovom prikazu svaki se brid unosi jednom
P = (E1,
E2, ..., E3)
i to na
sljedeći način:
E = (V1,
V2, P1, P2)
gdje su prva dva elementa koordinate vrhova koji određuju brid, a druga dva
elementa oznake mnogokuta kojima je taj brid zajednički. Mnogokut se prikazuje
iscrtavanjem bridova.
Ova metoda ilustrirana je primjerom na slici 3.22.
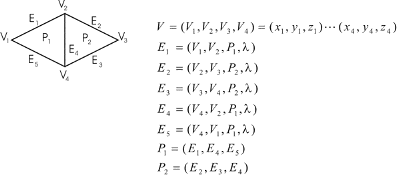
Slika 3.22 Mreža mnogokuta definirana pokazivačima u listu bridova.
Površine
drugog reda kao što su površina kugle, površina elipsoida ili cilindra mogu
poslužiti kao elementarne površine za definiranje modela složenijih površina u
trodimenzionalnom prostoru. Ova skupina površina definirana je implicitnom
jednadžbom oblika:
f(x,y,z)
= ax2 + by2 + cz2 + 2dxy + 2eyz + 2fxz + 2gx +
2hy + 2jz + k = 0
Vrsta površine određena je vrijednostima parametara a, b, c, d, e, f, g, h, i, j i k.
Prednosti ovog pristupa su prikladnost za niz proračuna kao što su normale na površinu u pojedinoj točci, određivanje presjeka, te određivanje pripadnosti točke površini. Ove prednosti temelje se na jasnoj matematičkoj formi definicije površine.
Povratak na: Početak stranice | Sadržaj
[The link bar feature is not available in this web] ||| Natrag: Crtanje primitivnih oblika | Gore: Matematički temelji računarske grafike | Naprijed: Crtanje trodimenzionalnih tijela |
Inženjerska grafika, Copyright © D.Begusic