12 OBRADBA SIGNALA

Uvod

Korelacija i autokorelacija

Fourierova transformacija autokorelacije

Autokorelacija derivacije funkcije

Korelacija (uzajamna korelacija)

Konvolucija

Princip holografije

12.5 Korelacija (uzajamna korelacija)

Funkcija korelacije signala x(t) i y(t) se definira izrazom:

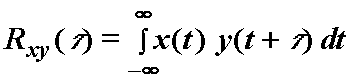(12.15)

Za diskretne signale x(n) i y(n) korelacija je dana izrazom:

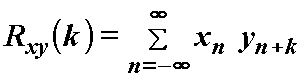(12.16)

Korelacija otkriva zajedničke karakteristike tj. sličnost, povezanost ili ovisnost funkcija x(t) i y(t).

Da li korelacija ukazuje na sličnost ili pak na povezanost odnosno ovisnost dviju funkcija ovisi o tome da li signali x(t) i y(t) dolaze iz različitih izvora ili iz istog izvora, ili je signal y(t) izlaz iz informacijskog filtra čiji ulaz je x(t).

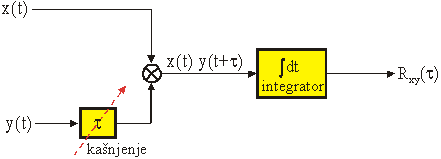
Slika 12.8 Analogna shema korelatora

Slično izvođenju izraza (12.9) za FT autokorelacije, za korelaciju vrijedi Fourierov transformacijski par:

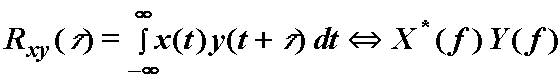
(12.17)

gdje vrijede FT parovi:

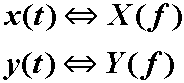
Zaključak: korelacija u vremenskom području odgovara množenju u frekvencijskom području gdje je prva gustoća kompleksno konjugirana

Ako se zamijeni redoslijed funkcija 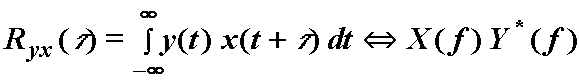(12.18)

Uz Fourierov transformacijski par zrcaljene funkcije prema (9.8) vrijedi:

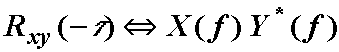(12.19)

Također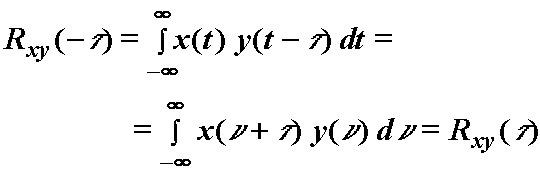

Dakle:

(12.20)

Slijedi da korelacijska funkcija nije općenito parna funkcija kao što je autokorelacijska funkcija. Korelacija će biti parna funkcija ako su x(t) i y(t) obje parne funkcije ili su obje neparne funkcije. Ovo slijedi iz (12.18) i (12.19). Vrijedi

što će vrijediti samo uz X(f) realno i Y(f) realno ili X(f) imaginarno i Y(f) imaginarno odnosno u vremenskom području uz x(t) i y(t) simetrične funkcije ili x(t) i y(t) nesimetrične funkcije.

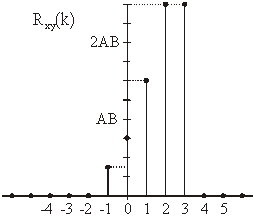
Primjer 12.4 Korelacija pravokutna i trokutna diskretnog impulsa

Neka su zadani diskretni signali x_n i y_n kao na slikama.

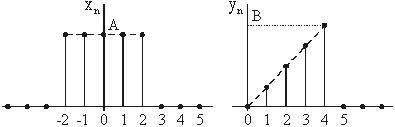
Iz izraza (12.6) slijedi:

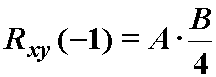
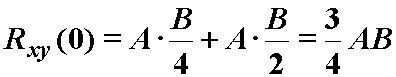
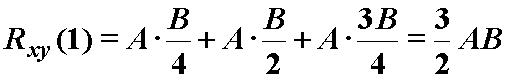
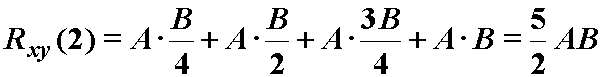
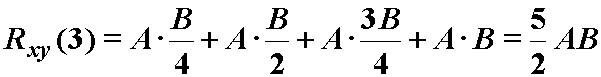
12.6 Konvolucija

Funkcija konvolucije se definira izrazom:

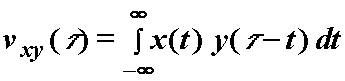(12.21)

ili simbolički:

(12.22)

gdje simbol označava konvoluciju.

U diskretnom obliku vrijedi:

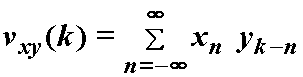(12.23)

Konvolucija je linearna, komutativna i asocijativna. Uz iz (12.21) slijedi:

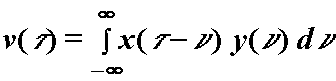
pa usporedba s (12.21) daje:

(12.24)

Lako je također pokazati da vrijedi:

(12.25)

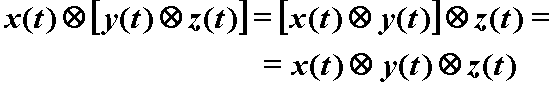(12.26)

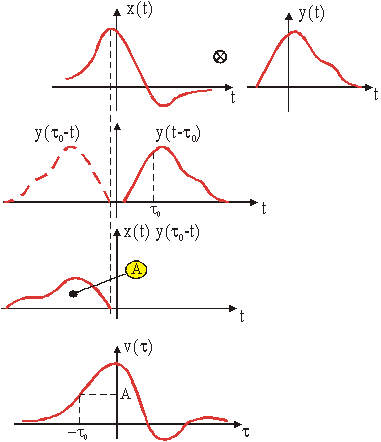
Proračun se konvolucije odvija slično rješavanju korelacije, osim što je jedna od funkcija zrcaljena. S obzirom na definiciju (12.21), rješavanje konvolucije teče sljedećim redom:

1. zrcaljenje funkcije čime se dobiva

2. pomak za čime se dobiva

3. površina umnoška daje vrijednost konvolucije .

Slika 12.9 Ilustracija računanja konvolucije

Fourierova transformacija konvolucijske funkcije se može lako definirati na temelju izraza (12.18) za korelaciju:

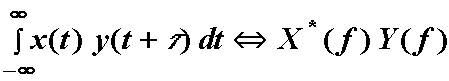
pa uz FT par (9.8):

slijedi:

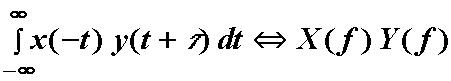
Uz vrijedi:

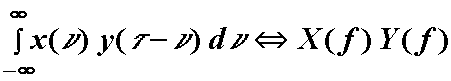
pa slijedi Fourierov transformacijski par za konvoluciju:

(12.27)

Zaključak: konvolucija u vremenskom području odgovara umnošku u frekvencijskom području.

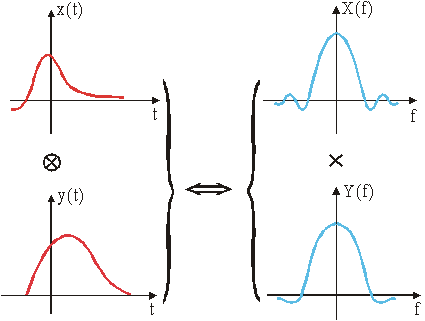
Slika 12.10 Ilustracija relacije (12.27)

U skladu sa simboličkim označavanjem konvolucije može se pisati simboličke izraze za autokorelaciju i korelaciju:

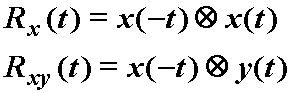(12.28)

Zanimljivo je također definirati konvoluciju u frekvencijskom području. Slično (12.21) vrijedi:

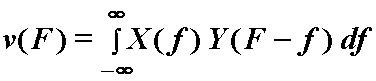ili simbolički

(12.29)

Nađimo IFT izraza (12.29):

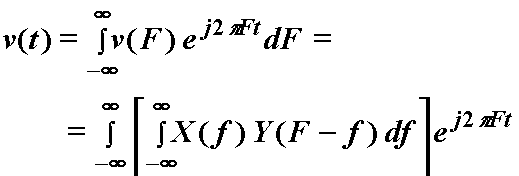
Uz slijedi:

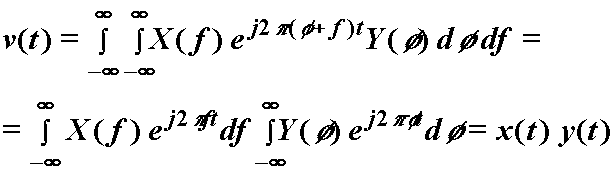
pa slijedi transformacijski par:

(12.30)

Zaključak: umnožak funkcija u vremenskom području odgovara konvoluciji u frekvencijskom području.

Za rješavanje složenijih problema u obradbi signala može se dakle koristiti sljedeće Fourierove transformacijske parove pisane preko operatora konvolucije:

1. Autokorelacija:

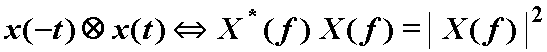
2. Korelacija:

(12.31)

3. Konvolucija:

4. Umnožak:

Zanimljiv je slučaj kad se traži konvolucija dviju funkcija gdje je jedna od njih jedinični impuls:

Neka je (jediničan impuls) pa (12.21) postaje:

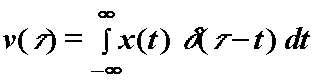
Uz :

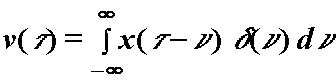
S obzirom na svojstvo (9.21) slijedi odnosno:

(12.32)

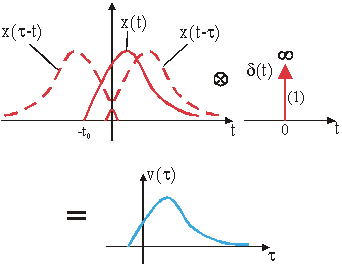
Slika 12.11 Ilustracija izraza (12.32)

Zaključak: konvolucija neke funkcije x(t) sa impulsnom funkcijom jednaka je samoj funkciji x(t).

Vrijedi dakle:

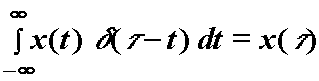(12.33)

Izraz (12.32) se može potvrditi rješavanjem u frekvencijskom području: Na temelju Fourierova para (12.27) vrijedi:

Budući vrijedi Fourierov par (9.22):

slijedi:

pa vrijedi:

odnosno:

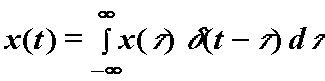(12.34)

Izraz (12.34) izražava funkciju x(t) kao linearnu kombinaciju impulsa . Relacija (12.34) je od temeljne važnosti u teoriji linearnih sustava (poglavlje 15).

Primjer 12.5 Konvolucija pravokutna i trokutna impulsa

Zadani su diskretni signali x_n i y_n kao u primjeru 12.4. Konvolucija je dana izrazom (12.23) a postupak rješavanja uključuje zrcaljenje y_n čime se dobiva y_-n pa slijedi pomak za što daje . Proračun v_xy(k) slijedi na isti način kao kod računanja korelacije u primjeru 12.4.

Jednostavniji put je preko spektralnih gustoća. Poredbom (12.27) i (12.19), a jer je x_n simetrična funkcija vrijedi , slijedi i .

12.7 Princip holografije

Holografija postaje sve više temelj trodimenzionalnoj (3-D) televiziji, videu ali i 3-D sustavima pohrane podataka. Optičke memorije temeljene na holografiji pohranjuju ogromne količine podataka. Međutim još je možda važnije svojstvo takvih memorija da oštećene ili čak razbijene u komadiće čuvaju cjelokupnu informaciju.

Holografija podrazumijeva trodimenzionalno (3-D) snimanje objekata na fotografsku ploču ili film odnosno na dvodimenzionalni (2-D) medij.

Fotografska ploča ili film pohranjuju samo energiju svjetlosnog vala, ali ne njegovu amplitudu i fazu. Holografski postupak omogućuje zapisivanje i faze signala ne mijenjajući tehnologiju snimanja.

U holografskom postupku koriste dva izvora svjetla: jedan kao i kod običnog snimanja a drugi kao referentni izvor.

Zbog jednostavnosti se princip holografije može promotriti na primjeru jednodimenzionalnih (1-D) signala.

Neka je x(t) vremenski ograničena funkcija x(t)=0 za t<t₀ i t>t₀+T kao na slici 12.12.

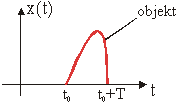
Slika 12.12 Vremenski signal kao objekt koji se snima

Slika 12.13 ilustrira postupak snimanja holograma. Pored običnog izvora svjetla koristi se i referentni izvor koji je lociran izvan objekta.

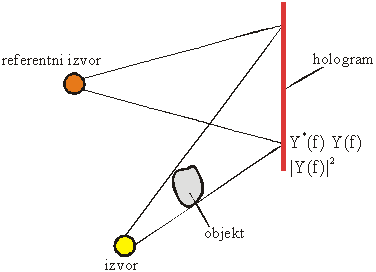
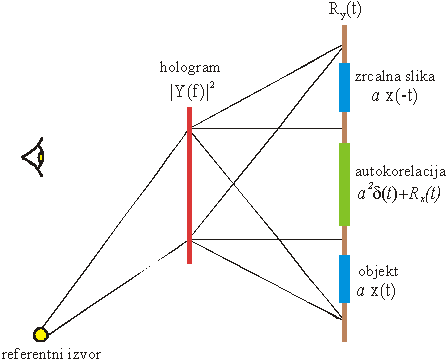
Slika 12.13 Postupak snimanja holograma

Slika 12.14 prikazuje ekvivalentnu situaciju svedenu na 1-D problem. Referentni izvor se u 1-D interpretaciji može prikazati kao jediničan impuls u t = 0.

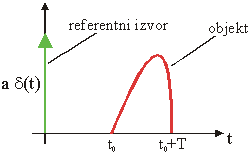
Slika 12.14 1-D interpretacija snimanja holograma

Na temelju slike 12.14 može se pisati:

(12.35)

U ravnini snimanja, signal odnosno slika odgovara Fourierovoj transformaciji (difrakcija uz Fraunhoffer-ovu aproksimaciju). To znači da snimak na filmu (hologram) predstavlja energijski spektar signala y(t) pa vrijedi:

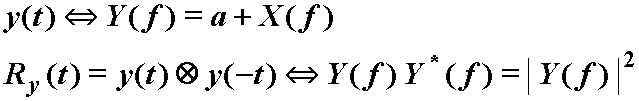(12.36)

Postavlja se pitanje da li se iz spektralne gustoće energije, tj. holograma, može dobiti originalni signal (objekt) x(t).

Nađimo autokorelaciju:

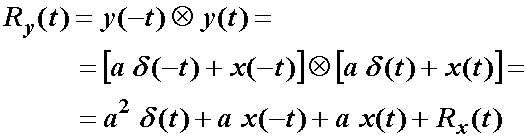(12.37)

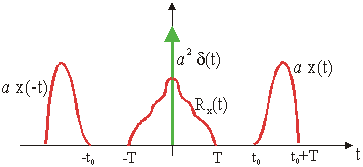
Slika 12.15 Autokorelacija signala definiranog izrazom (12.35)

Iz izraza (12.37) odnosno slike 12.15 je očigledno da mora vrijediti t₀ > T kako ne bi došlo do preklapanja slike objekta i njegove autokorelacije ili pak referentni signal mora imati veliku amplitudu tako da je utjecaj preklapanja R_x(t) malen.

Autokorelacija (12.37) predstavlja inverznu Fourierovu transformaciju holograma.

Slika 12.16 ilustrira ekvivalentni postupak 'računanja' IFT za stvarnu situaciju. Referentno svjetlo osvjetljava objekt i na zaslonu se dobivaju originalna i zrcalna slika objekta. Postupak se naziva i rekonstrukcija objekta iz holograma.

Slika 12.16 Rekonstrukcija objekta iz holograma